Dr James Park answers this very important question from a reader.
A reader asked about the distance to use to tune a recurve bow. It is an excellent question and is best approached by considering the aerodynamic behaviour of both fletched and unfletched arrows. I have considered that behaviour in considerable detail and have models of the dynamic behaviour both during the bow’s power stroke and then in free flight. I have tested those models against actual arrow behaviour. Some of this is covered in my published papers which you can find in the Journal of Sports Engineering and Technology (https://journals.sagepub.com/home/pip). I will use my Hoyt Formula recurve bow and X10s as an example in this article.
An arrow in free flight can be expected to be flexing in both the lateral and the vertical planes. In the lateral plane this is due to the way the string leaves the archer’s fingers. In the vertical plane it is due to the arrow pass usually being above the centre of the bow and consequently having a curved nocking point path – although usually this flex will be quite small. The flex amplitude decreases during the arrow flight but will still be significant even at the target distance.
The arrow can be rotating about its centre of mass in both the lateral and vertical planes (yawing and pitching in engineering speak). Consequently, the arrow shaft can have a non-zero angle of attack compared to the airflow. It should also be rotating about its longitudinal axis (roll in engineering speak) due to the fletch offset angle.
When we are tuning the bow, we are trying to minimise the yawing and pitching (minimising the fishtailing and porpoising in archer speak).
As well as the arrow’s centre of mass, we also need to consider the arrow’s aerodynamic centre. The position of the centre of mass is largely determined by the point mass compared to the mass of the rest of the arrow – it will be forward of the arrow’s geometric centre. The position of the aerodynamic centre is determined by lift and drag contributed by each part of the arrow – for any sensible arrow it will be behind the arrow’s geometric centre and will be dominated by the shaft and fletches. That is, the aerodynamic centre will be behind the centre of mass – this is essential as otherwise the arrow will turn around and fly backwards. Note that even for an arrow with no fletches the drag and lift from the shaft will (usually) ensure that the aerodynamic centre is behind the centre of mass – otherwise you could not successfully shoot an unfletched arrow.
If the arrow’s angle of attack to the airflow is not zero, the resultant lift and drag from the various parts of the arrow act to pull the arrow into line with the airflow. By far the largest contributor to this is the lift from the fletches, followed by the lift from the shaft. Since this movement is only lightly damped, the attack angle will overshoot zero and we will get an angle of attack in the opposite direction. The amplitude of the oscillation decreases as the arrow goes down range. Consequently, if we have an arrow oscillating in yaw (fishtailing) and we watch it carefully, we should be able to see it first angled to one side, then the other, and so on.
If the arrow is angled away from the airflow, the aerodynamic forces will have a component that pushes the arrow to the side. For example, if the rear of the arrow is to the left, the forces will push the arrow to the right as well as trying to rotate the arrow to be in line with the airflow. Then, when it overshoots, it will be pushed in the opposite direction, but since the oscillation amplitude is reducing, so will be the amount it is pushed on each successive swing.
The period of this oscillation depends on the rotational inertia of the arrow about its centre of mass and the magnitude of the forces. This means that a fletched arrow will react faster than an unfletched arrow. It is this difference that we use when we run a bare shaft test as it means that the lateral or vertical displacements of the arrow at the target will be different for the two cases.
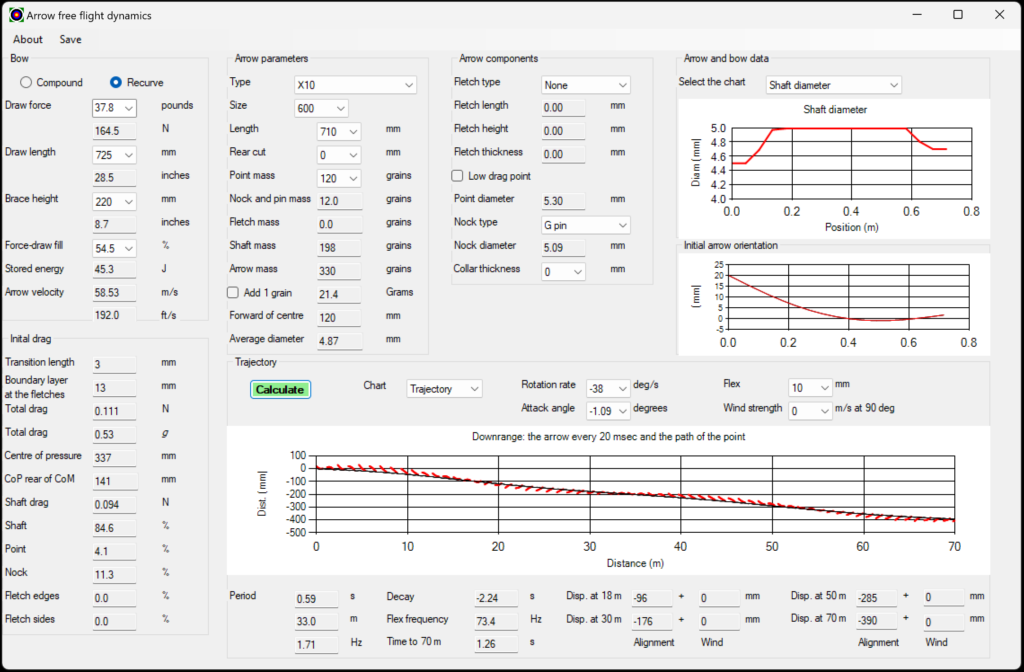
My Hoyt recurve bow and X10s tunes very nicely at a draw force of 35.8 pounds that gives a zero lateral rotation about the arrow’s centre of mass after the arrow leaves the bow, as desired, a small angle of attack of -0.76 degrees and an arrow flex amplitude of 9.4 mm. If I run my model for a draw force two pounds greater than that it shows that the arrow is now too weak (as expected). The arrow lateral rotation rate is then -9.7 degrees/second, the angle of attack to the airflow is -1.07 degrees, and the flex amplitude is 10.2 mm. This is as shown in the screenshot from my model in Figure 1.
Those values can then be used as the initial conditions for the free flight analysis, as shown in Figure 2, a screenshot from another of my models. In this case, the arrows were fletched using Spinwings. The down range behaviour for the unfletched arrow is shown in Figure 3. The lateral displacements at various target distances, from Figures 2 and 3, are shown in Table 1.
Table 1 shows that in each case the unfletched arrow hits to the right of the fletched arrow, as expected for a right-handed archer when the arrow is too flexible.
So, which distance should we use for our bare shaft testing? We need to have the best chance of being able to discern those differences.
We need to bear in mind the archer’s normal group size, and how it changes with distance. Note that two factors (variable bow cant and variable wind drift) increase as the square of target distance, so those factors point to the longer target distances not being as useful as the shorter distances. Note that the longer distances do not provide ‘increased tuning accuracy’.
At my skill level (about 340 for 6 ends at 30 m on an 800 mm target face), the standard deviation of my group at a target distance of 30 m will be about 35 mm, and It will be about 20 mm at a target distance of 18 m, so for both the differences above are well over 2 standard deviations. Hence, for both 18 m and 30 m I should be readily able to group well enough to see the difference in position of the fletched and unfletched arrows. Hence, I would be happy to use either target distance.
The Verdict
Which target distance do I actually use for my bare shaft testing? I usually use about 18 m as I can do that out of any wind. However, I also watch how my arrows fly (and from many years of practice I can see their behaviour quite well). I am able to see their behaviour better at longer target distance, so I like to do that at around 30 m on a still day. That is, the distance is not critical, but do not use extreme distances and, importantly when tuning, keep out of the wind.
Figures and tables by Dr James Park
Table 1. The lateral displacements at various target distances for the fletched and unfletched arrows.
| Displacement at 18 m | Displacement at 30 m | Displacement at 50 m | Displacement at 70 m | |
| Fletched | -44 mm | -77 mm | -132 mm | -189 mm |
| Unfletched | -96 mm | -176 mm | -285 mm | -390 mm |
| Difference | 52 mm | 99 mm | 153 mm | 201 mm |
Figure 1. The arrow behaviour as it leaves the bow with the draw force set 2 pounds too high
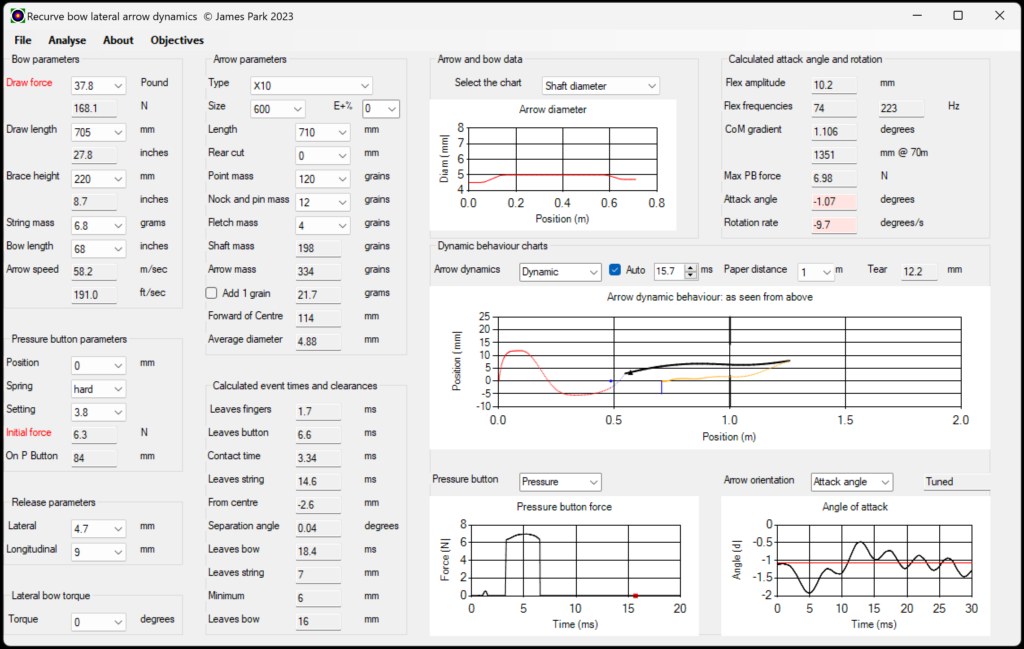
Figure 2. The down range behaviour with the fletched arrow and with the draw force 2 pounds too high.
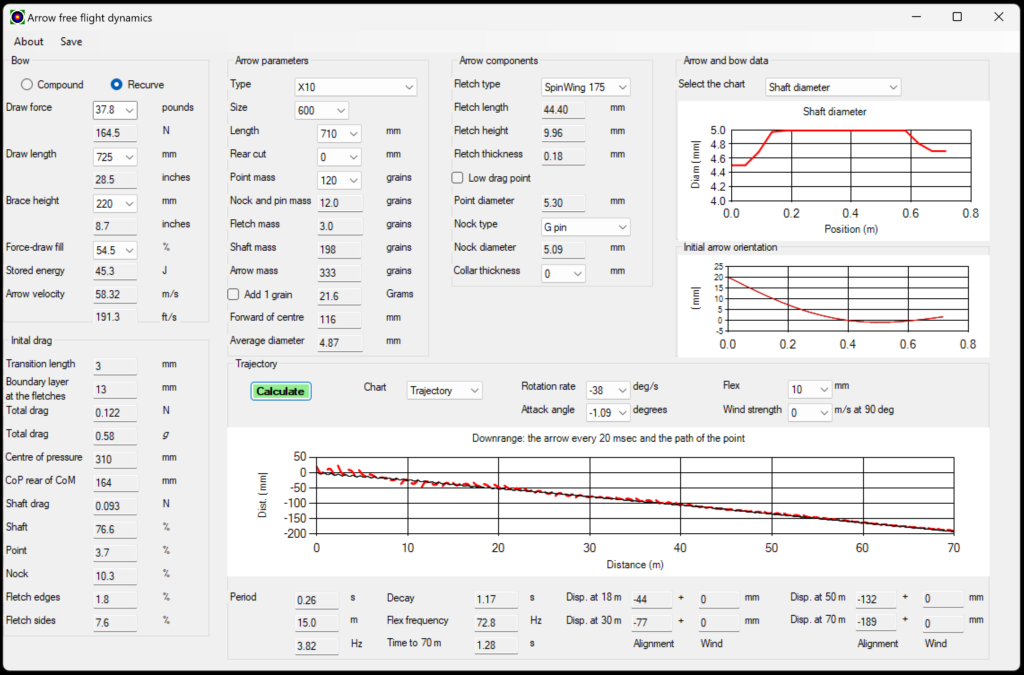
Figure 3. The down range behaviour with the unfletched arrow and with the draw force 2 pounds too high.